Measuring CPU cache line size using Python code
Published:
Estimating with a small experiment, the cache line size of a cpu (Apple M1 in this case) using Python code.
Introduction
Cache line size is the minimum size of memory that is loaded into the caches (L1, L2, etc) whenever an access of some information is requested from the memory. If we access say an element from a numpy array with dtype int8 (each element of size 1 byte), along with it, the cpu loads 127 bytes of information more that was not specifically asked for, as it comes at no extra cost, and it tries to load those pieces of memory, that it predicts might be requested soon (like say next few elements from the same array).
One can check the cache line size of their cpu on macOS using the sysctl command:
$ sysctl -a | grep cachelinesize
hw.cachelinesize: 128
It is an interesting exercise to estimate the cache line size using code, which I try to do below
Experiment 1: Accessing elements from array at different strides in hope of predicting cache line size
According to the explanation above, one may think that if we access n elements from an array at different strides, then the time taken for accesses at shorter strides, say stride = 1 should be smaller than larger strides, say stride = 1000. However, as we will see below, it seems like the times for both cases is same.
import numpy as np
import time
# function to access n items the array at different strides, and return the time taken to do so
def RecordTimeForAccess(stride = 1):
# it is important to create a new array for each test, because we don't want that the array's
# elements are already in cache, which might ruin our results.
arr = np.ones(shape = 100000000, dtype = np.int8)
starttime = time.perf_counter()
# loop through certain values and we will access those indices in arr
for i in range(0, 1+stride*10000, stride):
_ = arr[i] # simple access of an entry in the array
endtime = time.perf_counter()
return endtime - starttime
# I try to access the elements of the array at different strides. Hence, if continuous memory
# elements are loaded into memory for caching purpose, this should show some difference in
# time taken
RecordTimeForAccess(1) # 0.0029707499779760838
RecordTimeForAccess(129) # 0.0027174160350114107
RecordTimeForAccess(1000) # 0.0026666249614208937
The time is same likely because of CPU prefetching, which refers to the CPU trying to predict our next accesses and loading corresponding data into the cache instead of simply adjacent pieces of memory. Here, the pattern in which we are accessing the data is simple, just constant strides of memory, and the CPU is able to predict that easily and ruining our experiment. Hence we come up with a new setup.
Experiment 2: Accessing elements from array in random order, but from regions of array of different sizes
In order to do our test successfully we need to remove the confounding factor of CPU prefetching predictions. Hence, we necessarily access the array’s elements randomly, as then the CPU prefetching is not able to predict our next move. But we limit the regions of the array from which the random elements can be chosen. Hence, if we take the elements from a small localized part of the array, we would expect the access times to be shorter as they are likely stored in cache upon initial few accesses. And if the region of the array from which we are choosing random elements (same number of random elements, just from a larger sample space) is big, then the access times should be more as for most of the element accesses, data is being moved from the memory freshly. This is what we try to do below:
# So I will create a function in which we create an array just like in the prev function
# RecordTimeForAccess, and then, we access the 0-indexed element from the array, and then
# 31 random elements from the array. However, we would have the option to specify that these
# 31 random indices are within what range of indices (and we make sure that there is no index
# repeat, just to highlight a bit more, the effect of cached elements instead of same element
# only). This way, we are fooling cpu prefetcher by accessing elements in random order, and
# can highlighting cache effects by limiting the random indices to just the start of array,
# and vice-versa.
# index_range_end - index_range_start should be greater than equal to 31
def RecordTimeForAccess2(index_range_start = 1, index_range_end = 128):
arr = np.ones(shape = 1000000, dtype = np.int8)
# create indices_to_access
indices_to_access = [0] # start with appending the 0, so that upon the first access, the first 128 elements of the array are stored in l1 cache
# now, according to supplied parameter (range of values), choose random 31 elements
all_possible_indices = np.arange(start = index_range_start, stop = index_range_end)
# choose 31 random elements from all_possible_indices and append to indices_to_access
indices_to_access += list(np.random.choice(a = all_possible_indices, size = 31, replace = False))
starttime = time.perf_counter()
# loop through certain values and we will access those indices in arr
for i in indices_to_access:
_ = arr[i] # simple access of an entry in the array
endtime = time.perf_counter()
return endtime - starttime
# now, lets record the time for 32 accesses in case of random indices but just from the
# first 128 elements of the array
time_taken = 0
for _ in range(1000):
time_taken += RecordTimeForAccess2()
time_taken # 0.00712 for 1000 iterations
# now, when the 128 random elements can be from far away parts of the array
time_taken2 = 0
for _ in range(1000):
time_taken2 += RecordTimeForAccess2(1, 100000)
time_taken2 # 0.01410 for 1000 iterations
As we can see, the time taken for 32 element accesses (1000 iterations of it) taken randomly in range (0, 100000) is around double of the time taken for 32 element accesses taken randomly in range (0, 128). However, we still haven’t estimated the cache size. For that, the following code helps:
import matplotlib.pyplot as plt
# now, lets try to vary the range from which we get 127 random elements in the array. Hopefully
# this would increase gradually, starting at 128, and indicate to us that the cache line size
# is 128 bytes
times_for_different_index_ends = []
for index_range_end in np.arange(start = 32, stop = 1000, step = 5):
time_taken2 = 0
for _ in range(1000):
time_taken2 += RecordTimeForAccess2(1, index_range_end)
# print(f'{index_range_end}: {time_taken2}')
times_for_different_index_ends.append(time_taken2)
plt.scatter(x = np.arange(start = 32, stop = 1000, step = 5), y = times_for_different_index_ends)
plt.show()
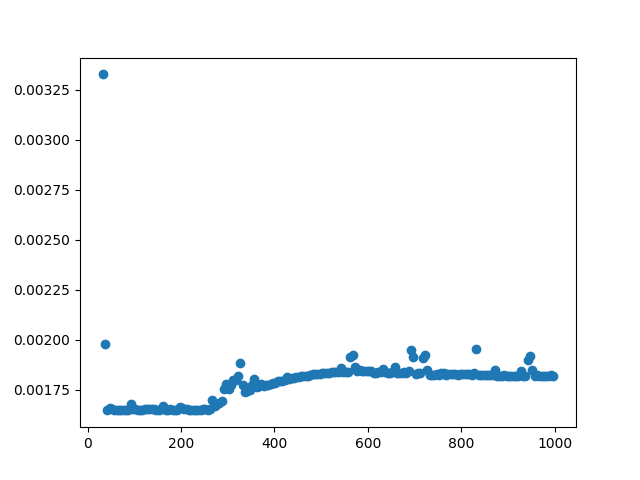
One thing that matches expectation is that for the first few range-end values, the access time is same. This implies that we have all the data in cache after the first element access (as we access the 0th element first in function RecordTimeForAccess2 and then randomly thereafter), and hence access is superfast (from cache).CPU prefetching is likely not playing any helping hand here as the elements are accessed randomly.
Post a certain point, the times start to increase gradually, implying more accesses of data from memory, because they are not all in cache (atleast straight after the first element access), which is also what we expected.
The thing that doesn’t match expectation is where the times start increasing. I would have expected this to be ~128, but it seems to be ~256. I am still thinking about this.
Overall, this was a good exercise playing around with data storage in cpu, and learning about its intricacies.
